Kevin Drum approvingly posted this chart from Muller:
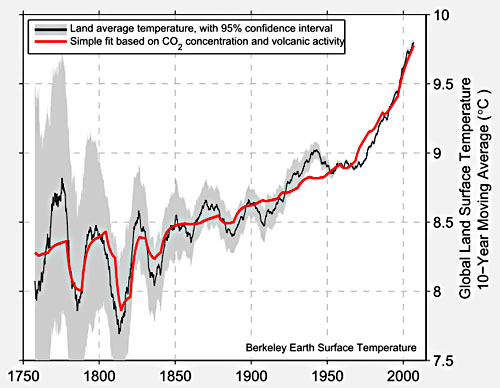
I applaud the effort to match theory to actual, you know, observations rather than model results. I don’t have a ton of time to write currently, but gave some quick comments:
1. This may seem an odd critique, but the fit is too good. There is no way that in a complex, chaotic system only two variables explain so much of a key output. You don’t have to doubt the catastrophic anthropogenic global warming theory to know that there are key variables that have important, measurable effects on world temperatures at these kind of timescales — ocean cycles come to mind immediately — which he has left out. Industrial-produced cooling aerosols, without which most climate models can’t be made to fit history, are another example. Muller’s analysis is like claiming that stock prices are driven by just two variables without having considered interest rates or earning in the analysis.
2. Just to give one example critique of the quality of “science” being held up as an example, any real scientist should laugh at the error ranges in this chart. The chart shows zero error for modern surface temperature readings. Zero. Not even 0.1F. This is hilariously flawed. Anyone who went through a good freshman physics or chemistry lab (ie many non-journalists) will have had basic concepts of errors drilled into them. An individual temperature instrument probably has an error when perfectly calibrated of say 0.2F at best. In the field, with indifferent maintenance and calibration, that probably raises to 0.5F. Given bad instrument sitings, that might raise over 1F. Now, add all those up, with all the uncertainties involved in trying to get a geographic average when, for example, large swaths of the earth are not covered by an official thermometer, and what is the error on the total? Not zero, I can guarantee you. Recognize that this press blitz comes because he can’t get this mess through peer review so he is going direct with it.
3. CO2 certainly has an effect on temperatures, but so do a lot of other things. The science that CO2 warms the Earth is solid. The science that CO2 catastrophically warms the Earth, with a high positive feedback climate system driven to climate sensitivities to CO2 of 3C per doubling or higher is not solid. Assuming half of past warming is due to man’s CO2 is not enough to support catastrophic forecasts. If half of past warming, or about .4C is due to man, that means climate sensitivity is around 1C, exactly the no-feedback number that climate skeptics have thought it was near for years. So additional past man-made warming has to be manufactured somehow to support the higher sensitivity, positive feedback cases.
Judith Curry has a number of comments, including links to what she considers best in class for this sort of historic reconstruction.
Update: Several folks have argued that the individual instrument error bars are irrelevant, I suppose because their errors will average. I am not convinced they average down to zero, as this chart seems to imply. But many of the errors are going to be systematic. For example, every single instrument in the surface average have manual adjustments made in multiple steps, from TOBS to corrections for UHI to statistical homogenization. In some cases these can be calculated with fair precision (e.g. TOBS) but in others they are basically a guess. And no one really knows if statistical homogenization approaches even make sense. In many cases, these adjustments can be up to several times larger in magnitude than the basic signal one is trying to measure (ie temperature anomaly and changes to it over time). Errors in these adjustments can be large and could well be systematic, meaning they don’t average out with multiple samples. And even errors in the raw measurements might have a systematic bias (if, for example, drift from calibration over time tended to be in one direction). Anthony Watt recently released a draft of a study I have not read yet, but seems to imply that the very sign of the non-TOBS adjustments is consistently wrong. As a professor of mine once said, if you are unsure of the sign, you don’t really know anything.

” An individual temperature instrument probably has an error when perfectly calibrated of say 0.2F at best…”
OK, sure, but the error bars in the graph are not the error of a single instrument, it is the error in the average. This error will decline with the square root of the number of instruments (approximately). I’m not saying Muller is right, but your focusing on the error of a single instrument seems to miss the point.
But it doesn’t match the first half of the 20th century! Where did the heat come from and why isn’t this failure so obvious to everyone? On top of that, a deg and a half in 250 years coming out of a climate minima? BFD.
There is NO greenhouse effect, of increasing temperature with increasing atmospheric carbon dioxide. When you write, “…if half of past warming is due to man”, you are promulgating Anthony Watt’s latest publicity, equally as cheesy as Muller’s. Watts is a dedicated “lukewarmer”, just as you seem to be, dedicated to making everyone think the CO2 climate sensitivity is about 1°C/doubling. The trouble is, it clearly is not, as shown at the above link in the comparison of temperatures in the atmospheres of Venus (with 96.5% CO2) and Earth (with just 0.04%): Venus’s temperature vs. pressure curve is right on top of Earth’s, when corrected for Venus’s closer distance from the Sun; if there were a greenhouse effect, Venus’s curve would be above Earth’s, by over 11°C according to “lukewarmer” understanding (1°C/doubling) or over 33°C according to IPCC-promulgated alarmist propaganda. The curves are RIGHT on top of each other (except inside the Venus cloud layer, where Venus’s falls BELOW Earth’s by a few degrees, never higher as expected from greenhouse theory). 97% of even skeptics are incompetent in this, because my comparison should have been done by any competent climate scientists 20 years ago, and the greenhouse effect dropped from science then. Lukewarmers, look at the Venus/Earth temperature comparison, and understand that is the definitive evidence that destroys any reasonable belief in the greenhouse effect. There simply is now no competent climate science, based as it is on that effect.
You wrote “real scientist should laugh at the error ranges in this chart,” and the reason you gave is that *individual instruments* have larger errors. When I (and others) pointed out the problem with this reasoning, you suddenly switch arguments to say you were talking about systematic errors, homogenization, etc. (BTW, according to Muller his project doesn’t even use homogenization.)
You just lost a lot of credibility with me. Muller decides to take an open-minded and skeptical look at the evidence, and decides to change his mind. And you casually dismiss him with a completely specious argument, including name calling (not a “real scientist”…in fact Muller is a “real scientist,” with a distinguished career in science unrelated to climate). Do you have any evidence that his project is insincere? Why so quick dismiss his work, rather than taking it seriously?
I am a long time reader of this site, and I share many of your concerns and frustrations about the way this whole debate has gone, and how prominent climate scientists and the press treat any opposing views. But I’m very disappointed with your reaction here.
I have a question that I’ve never found a satisfactory answer to. Measurement sites form the core input of the data set for calculating this “global mean temperature” (whatever that actually means), but the measurements from these sites is accurate at best to the nearest 1 degree, in actual practice around the nearest 5 degrees since many are reading off mercury thermometers — and this condition increases in frequency the further back in time you go. Now, given that the least significant digit of the input data is integer 1, or for later data integer 5, then how do you calculate a “result” based on this data has a GREATER accuracy than the input data — specifically, the claim that this calculated “global mean temperature” has increased by fractions of a degree celsius, and typically reported to the 0.00 degree accuracy. This is mathematically impossible — you cannot get more accurate calculated results than the accuracy of the data used as the input. You can assume, as noted above, that “errors cancel out” — a very specious assumption by the way — but even if you grant that, it still doesn’t magically transform the input data from being accurate to say 10 degrees Celsius to 10.86 degree Celsius — it just says you assume away the fact that the actual value could be anywhere on the interval [9,11] degrees Celsius or alternatively [5,15] degrees Celsius. So how do you then calculate something that presumes you knew, with absolute clarity, that the value was precisely 10 degrees — without that result having an equal, or even higher, error bound on it? And at an accuracy of integer 1, it means that the “global mean temperature” could actually be anything from [0,1], or [-1,1] depending on whether you round that 0.00 to integer first.
You say “The science that CO2 warms the Earth is solid.”
I say “No, it’s not.” By that I mean that many skeptics, myself included, don’t buy the popular model that the cause of earth’s warming is the re-readiation of solar energy by CO2 molecules in the atmosphere. There are experimental results that purport to prove this on both sides. But the science is far from ‘solid,’ as far as I can tell.
Short answer: the errors cancel out (or almost entirely cancel out, depending on plausible assumptions about the distribution of the underlying true temperatures).
If you don’t believe me, do the math yourself, it’s basic statistics. Or run a simulation…you could even do this in excel.
No, because you are assuming the errors are distributed in a Gaussian fashion or some other such uniform profile. You can assume that — you have no way of actually knowing or proving that other than a desire for it to be so since it supports the premise of the outcome, and a non-Gaussian distribution pretty much blows the whole calculation out of the water. So, 3rdMoment — what evidence do you have to prove your assumption of uniform distribution of errors is correct?
No, because you are assuming the errors are distributed in a Gaussian fashion or some other such uniform profile. You can assume that — you have no way of actually knowing or proving that other than a desire for it to be so since it supports the premise of the outcome, and a non-Gaussian distribution pretty much blows the whole calculation out of the water. So, 3rdMoment — what evidence do you have to prove your assumption of uniform distribution of errors is correct? For example, as sites are place near population centers at a greater rate, the deviation from true temperature is not Gaussian — it becomes skewed in favor of hotter readings as you get closer to the current date, or alternatively cooler as you go further back in time. That’s just one example of how you get non-Gaussian error distribution in the data.
Wrong, I am making no assumption about anything being gaussian or uniform, or anything like that. You were talking about the error caused by rounding the true temperature up to a whole number (or a number divisible by 5). This error will have a distribution that will depend on the underlying distribution of temperatures, but it will be uncorrelated, or very close to uncorrelated, with the underlying true temperature for any reasonable assumption about true underlying temperatures (please note I said uncorrelated, not independent, since they will certainly not be independent). This is enough for the errors to cancel out.
Again, please do the math, or a simulation, and you will see.
(Don’t know why you are bringing in biases due to urban effects and such, as these were not a part of your original question I was attempting to answer.)
I guess I inelegantly worded the original premise by using the measurement error as an example, so it appeared to be the core of my question. It wasn’t — so that’s my fault. So to clarify — what I’m asking is, how do you get a result that supposedly has more significant digits of accuracy than the input data on which that result is based? Then…for example, measurements from thermometers in the earlier sections of the data could be at best accurate to the integer degree or five degrees — it is not accurate to the 0.00 degree. Yet a “global mean temperature” is calculated, and the difference between two such calculations from data sets from different years, is suppose to be accurate to the 0.00 level. Now the argument is typically advanced that “all errors will balance out, therefore it really is accurate to the 0.00 level because I assume I get absolute accuracy by aggregation and error cancellation”. My point is — they don’t, or at least you have no way of demonstrating they do beyond faith and hope.
That’s the point of my question — how do you claim to get 0.00 accuracy in order to claim that you know, for a scientific fact, that a “global mean temperature” for say 1940 can be calculated, compared to a “global mean temperature” for 2010, and the “difference” is 0.75 degrees Celsius, when the inputs aren’t accurate to that level? And if they aren’t — if you concede they can’t be — then the entire output of the whole man-made global warming analysis is pointless — because they claim differences of around 0.8 degrees Celsius, and make further claims of being able to detect even smaller changes in 1980-2010, within decade, and even between-years.
OK, I’ve spent too much time on this, but here’s a sketch of the math:
Assume the underlying temperature will be some fractional number, but the measuring device will round it off to the nearest degree. This “rounding error” is what we are concerned with. Sometimes this error will be positive (like when the true temperature is 28.8 and it gets rounded up to 29) and sometimes negative (like when the true temperature is 14.3 and it gets rounded down to 14). But as long as the true temperatures are distributed more or less continuously and smoothly over a wide range, the “expected value” of the rounding error in a randomly selected observation will be very very close to zero. Therefore, by the law of large numbers, these errors will mostly cancel out as the number of observations gets large (in other words the average of the errors will be very close to zero). Thus the average of the rounded observations (note that this average will be a fraction even though each observation is a whole number) will be very close to the average of the true temperatures as the number of observations gets large.
And that’s where the disconnect is. “Assume the underlying temperature will be some fractional number, but
the measuring device will round it off to the nearest degree.” — you assume that. It isn’t. It’s demonstrable by inspection that it isn’t.
“Sometimes this error will be positive (like when the true temperature is
28.8 and it gets rounded up to 29) and sometimes negative (like when
the true temperature is 14.3 and it gets rounded down to 14). But as
long as the true temperatures are distributed more or less continuously
and smoothly over a wide range, the “expected value” of the rounding
error in a randomly selected observation will be very very close to
zero.” — Again, it isn’t. You assume it is. It’s demonstrable by inspection that biases are not “distributed more or less continously and smoothly”.
You’ve answered my question, whether intentionally or not. The answer is, man-made global warming supporters simply wave their hands in the air, assume Gaussian or near-Gaussian distribution of errors from a multitiude of very complex, biased sources, declare they cancel out, and that aggregation and division allow them to generate a result with 0.00 accuracy even though the input data cannot be measured to that degree of accuracy. Parts of the data may have some elements of the errors that are Gaussian — the example of measurement error in terms of scale may be Gaussian — after get through the problems of variances in the thermometers themselves, which is also a well-known problem for mercury thermometers vis a vis their manufacturing — but their measured variance from the true temperature is not demonstrably Gaussian, and gets worse the further back you go. And the totality of the errors are not definitionally Gaussian — and are not demonstrated to be so.
The law of large numbers requires data sources to be free of bias, and the errors to be Gaussian in distribution. I fail to see where the assumptions are met given the nature of the input data. You keep repeating, over and over, the mathematics of the law of large numbers — or rewording thereof, e.g. “the errors cancel out” — but you never demonstrate how the fundamental assumption of Gaussian distribution of errors is proven — you simply take as an article of faith it is.
I never assumed anything Gaussian. The law of large numbers absolutey does not require Gaussian, or any particular distribution, that’s just wrong. Get your theorems straight and learn to read. We’re done here.
Mmm…nope, you’re still wrong. The inherent assumptions of the law of large numbers is that all possible outcomes are known, and there are no inherent biases in the system. The most oft-cited examples are the roll of a fair dice and the flip of a fair coin. The literal law is that if you do an experiment over and over enough times, you will converge to the expected value. It is always predicated with the caveat “fair” running of the experiment – no systemic biases. It is therefore inherently assumed that errors are Gaussian – otherwise, if they don’t cancel out over large numbers, then the calculated number is biased and incorrect.
It is also inherently assumed that you are rerunning the exact same experiment every time. Therefore, I’m actually being generous in considering that law, because it actually doesn’t hold for this question. In order for this to really hold, you would have to repeat readings at each individual recording site, a large number of times, in a way that holds all other variables constant. Taking a measurement in April, another in July, or even a continuum of numbers from April to July, do not meet the law of large numbers if the surrounding environment is altered, such as cars parked nearby. It does, in fact, definitionally assume Gaussian distribution of errors in order to allow you to ignore them. It just sounds nice to appeal to it because the subject happens to have a large data set – but that does not equate to it holding to the law of large numbers when those numbers are not derived from the same experimental conditions. But for a superficial discussion, I don’t mind it because it does demonstrate the fundamental crux of your approach – you inherently assume errors cancel out and it goes to absolute accuracy. That assumption is flawed. Perhaps you should get your theorems straight and learn to read. You don’t even apply the law of large numbers correctly in the first place.
Off topic but interesting.
The alarmists are alarmed [?] that the grace satellite shows Antarctica to be losing 260 billion tons of ice a year.
Since there are 27 million billion tons it will take 10 billion years to sublimate. it is too cold to melt.
Was Muller actually a “skeptic” of AGW? I recall the presentation he gave when he announced this study (I can’t find it at the moment but hoping someone else here also watched) where he stated that he human activity is the primary cause of GW, but the current (at the time) science was sloppy, thus he aimed to prove what he already suspected to be true. Anyone else watch this presentation?
No one has invoked “chaos theory”. “Green-house GASES ” ARE the issues of global climate instability with record global snow in odd places, floods drought and F’in heat waves. Natural rythyms combined with manmade emissions have caused some degree of instability.That is Fact. Next Fact: PEAK-OIL. will you deny this too. or will it be written off as hocus-pocus too. You can fill my email with all your crazy nonsense at_ bmok4usa@cox.net lets hear whatcha got!!!!