While I am big proponent of the inherent superiority of satellite temperature measurement over surface temperature measurement (at least as currently practiced), I have argued for a while that the satellite and surface temperature measurement records seem to be converging, and in fact much of the difference in their readings is based on different base periods used to set the "zero" anomoly.
I am happy to see Anthony Watt has done this analysis, and he does indeed find that, at least for the last 20 years or so, that the leading surface and satellite temperature measurement systems are showing about the same number for warming (though by theory I think the surface readings should be rising a bit slower, if greenhouse gasses are the true cause of the warming). The other interesting conclusion is that the amount of warming over the last 20 years is very small, and over the last ten years is nothing.

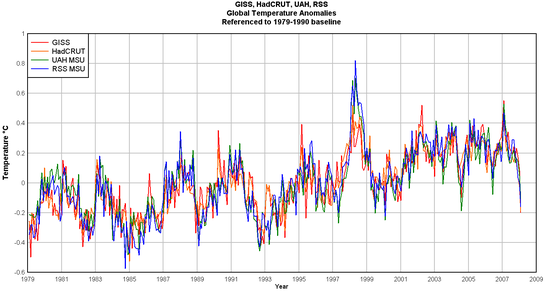
You claim to have argued for a while that the satellite and surface temperature measurement records seem to be converging, and yet not very long ago you were slating anyone who thought surface measurements were valid, saying that the surface temperature readings give them the answer they want, rather than the answer that is correct. As you have now demonstrated, surface and satellite measurements give the same answer.
How on earth do you conclude that the amount of warming over the last 20 years is small and over the last 10 is nothing? Do you actually look at the data? From the GISTEMP numbers, the five year average anomaly centred on 1985 was 0.23°C. The value centred on 1995 was 0.35°C and that centred on 2005 was 0.68°C. I see a pattern in those numbers. Do you?
Scientist, please go to http://vortex.nsstc.uah.edu/data/msu/t2lt/uahncdc.lt, plot the monthly global temperature anomaly data from Feb. 1998 through Jan. 2008 (10 years), and tell me the slope of a linear regression line for that data set. I get 0.005 deg C per year. Doesn’t that sound rather like nothing?
Now, I think a case could be made that starting the data set at 10 years ago is a little bit of cherry picking since 1998 was a warm El Nino year. To me, it is much more telling that there has been zero warming since Jan. 2001. (You can prove this to yourself using whatever global monthly anomaly data set from Jan. 2001 to present you like, even this one: http://data.giss.nasa.gov/gistemp/tabledata/GLB.Ts+dSST.txt) In other words, we have had 7 years of zero warming while CO2 concentrations have been increasing, which I find interesting considering the AGW alarmist position that CO2 is the prime influence of global temperature. Obviously, something else has had at least an equal amount of influence for the past seven years. It would be nice to have a clearer understanding of what that is. Which is why the AGW alarmist mantra of, “The science is settled.” is so absurd.
Scientist, beyond all else, converging does not imply they’re the same – quite the contrary, it implies that the trend is that they will eventually BECOME the same. Converged would be the state in which both give the same answer – converging means the answer is still to some extent different.
Incidentally, talking about cherry picking data – take a look at the graph, at 1985, 1995, and 2005. You’ve chosen a local(Well, regional, but I’m thinking in spite of all evidence to the contrary that you can grasp the intent) minimum for 1985, a period halfway up the slope between a local minima and maxima for 1995, and a fairly average set of temperatures for 2005. This only works if you DO use a five-year average – if you use a ten-year average centering on these years, the answer becomes a lot less impressive. (And if you just use a five-year average and include the two data points you left out – 1990 and 2000 – your trend vanishes entirely.) 1985 then includes more than a strong local minimum, 1995 comes to include the El Nino, and 2005 – well, you can’t do it for 2005, because the data set is smaller. You’ll have to wait two more years before using those center points, which sort of begs the question of why they were even used. (More cherry picking, perhaps?)
Scientist,
Firstly, you have to consider how those changing means compare with the stochastic variability in the data. I toss a coin 1000 times and count the number of heads minus the number of tails. (Well, OK, I simulated doing that using the Excel random number generator.) After 800 tosses the total is 16, after 900 tosses the total is 37, after 1000 tosses the answer is 49. I spot a pattern. Do you?
Secondly, taking the slope of a linear regression makes an implicit assumption that the underlying behaviour is a linear slope plus zero-mean iid Gaussian noise. What if it isn’t? When I look at the data, I see step changes. This is particularly clear if you plot the difference between northern and southern hemispheres against time. There’s a step change in behaviour in the mid 90s, coincident with the change in sign of the AMO, that is immediately followed by that big El Nino spike looking remarkably like a Gibbs effect overshoot and ‘ringing’. The data is too noisy to be sure, though.
So if the underlying behaviour is of horizontal steps plus autocorrelated noise, it’s perfectly possible to say the last 10 years there’s been no change (without committing oneself to saying anything about which way the next step will go), and taking a linear least-squares regression fit would be a totally inappropriate thing to do.
If, on the other hand, the claim is that the underlying trend is a smooth function with iid Gaussian noise, then the linear fit is just estimating the derivative at that point. That’s OK, but now you have to be careful about the bandwidth of the signal. Take the fit over too long a time interval, and you chop off the high frequencies and lose as much information as you gain by averaging over more points. That’s an additional bunch of assumptions or potential sources of error that you have to justify. And if the actual signal really is high-bandwidth, as step changes would be, you risk throwing away any data that might contradict your hypothesis, building in a sort of confirmation bias into your method.
Whether the temperatures converge or not, I would still regard satellite as far superior, and regard anyone who used the surface record in preference to the satellites for studying current global trends as suspect. The only decent reason for using the surface data is for compatibility with the record before 1978.
Keith – yes, starting in 1998 is just not going to give a useful answer, because global temperatures in that year were elevated enormously above the mean by the El Niño. And trying to claim anything based on temperatures since 2001 is also not useful. Random internal variations dominate on that timescale. You don’t need to seek some other factor to ‘negate’ CO2 as you seem to think. Here’s an exercise you can do to show this. Use a spreadsheet to generate a series of numbers, in which the average value rises by a value x per unit time, and the standard deviation is 5x. You know, a priori, that the trend is upward. If you plot seven-step trend lines, you’ll find plenty of flat or even downward pointing ones. Would you use those to argue that the underlying trend really is actually non-existent or downward?
Adirian – look at the graph in the post. Do those four lines look to you like they are ‘converging’, or do they look more like they are identical to within the errors? And here are the ten year average global temperature anomalies centred on 1983, 1993 and 2003 (so that we are using the most recent data possible) – 0.21°C, 0.35°C, 0.63°C. And here are the five-year averages centred on 1985, 1990, 1995, 2000 and 2005: 0.23, 0.34, 0.35, 0.57, 0.68. Somehow you think those numbers don’t show a trend?
Stevo – I think this graph shows very well that a linear trend plus noise in a normal distribution about the mean is a good characterisation of temperature trends over the last 30 years. You’re right about the need to select an appropriate fitting window though. I’m sure we both agree that seven years is way too short as noise will dominate.
Scientist,
That’s exactly the sort of thing I mean. Those look like annual averages, which means you’ve effectively put it through a moving average filter and sampled the result, which means you’ve thrown away a whole lot of high-frequency information. That’s fine if your statistical model is correct and that part of the spectrum consists entirely of error, but it doesn’t help to prove it. To take an extreme example, I could average the first half of the data and the second half, plot the two points, and claim the perfect straight line between the two was proof of a linear relationship. It’s an obvious nonsense.
What you have to do is to look at the residuals between the raw data and your smoothing, and show that there’s no time-dependence in it. (e.g. like the Durbin-Watson test.)
I agree that over a short time interval like seven years, noise will dominate. What isn’t so clear is that extending that interval will necessarily improve things. You have a signal you’re looking for with a particular frequency spectrum. It has noise added to it with its own frequency spectrum. You have to filter the result to drop those frequencies where noise dominates, while keeping those for which the signal dominates. You get some error from both noise getting through the filter, and the signal being blocked. The concern in this case is that the noise is red, and skewed towards low frequencies. That means that filtering doesn’t do as much good as you might think, and that a lot of what gets through your smoothing/averaging low-pass filter is not necessarily signal. It’s possible that you can never get any improvement by filtering, if the spectra of signal and noise are similar shapes.
Consider my example of cumulative coin tosses again. I can take a continuous block of several hundred points, average in groups or otherwise smooth it, and get what looks like a nice, linear trend that rises steeply. It would look virtually identical to Tamino’s graph. And yet, the mean of the actual distribution at every point is identically zero – there is no trend. What’s more, my smoothing would have eliminated the visible autocorrelation structure that would have given someone who knows about it the clue that more caution is needed. There are mathematical methods applicable to wide bandwidth signals in autocorrelated noise, but eyeballing graphs isn’t one of them.
In your example of a linear upwards trend in 5x noise, you mention that sometime the calculated trend may be downwards. You are right that you cannot use this to claim that it’s really zero or down – but what you can do is to say it isn’t statistically distinguishable from zero or down. There’s no evidence to say it’s up. Draw error bars round your gradient estimate, and you’ll find they overlaps zero, so if your null hypothesis is that there’s no change, it cannot be rejected. This problem is enormously magnified in the case of autocorrelated red noise, because all the usual estimators of the variance tend to underestimate it. In effect, you have 5x variance that looks from the wiggles on the graph like 1x variance.
No part of the sceptical argument hangs on this – virtually all sceptics freely confirm that the global mean temperature has risen over the past century and a half, so if it was still rising, it wouldn’t bother us. I should say that over the 20-50 year range we all agree there is an increase in temperature. But the trend you get depends on what time interval you take. Why is 30 years necessarily any better than 10 years, or 70 years, or 1000 years? Over the last ten years there is, statistically, no trend. That is just as valid a statement to make as that over the last 30 years there is. Without a proper understanding of the statistical properties of the natural variation, none of these statements has any significance.
Scientist – I would agree they show a trend, and I would argue further about that – however, I find it too bizarre that you’re arguing in the same context that 33% of the data we’re discussing should be ignored due to internal variability. What’s even the point of bringing up data if you don’t even consider it reliable? (And if ten years of data can be discarded because “random variability” means you don’t get the answer you want, is it that much of a stretch to discard fifty because it doesn’t give the answer we want? What is the difference? It seems that, either way, what is really being asked for is more time for the point to be proven.)
Adirian – where did I say ignore 33% of the data? Where did I say the data was not reliable?
Stevo – I think that if you looked at any ten year period in the instrumental record, you’d find that statistically the trend was indistinguishable from flat, or only barely so. A good reason that 30 years is a better time period to calculate a trend is that the trend calculated is statistically significant, and physically meaningful. Physically, the timescale we look at tells us something about the forcings operating on those timescales. On a timescale of a few years, most of the variation is unforced, ie internal. This is interesting to weathermen, but not to climate scientists. On a timescale of millions of years, most of the variation is due to long slow changes in Earth’s orbital configuration and continental movements – interesting to astronomers and geologists but with little bearing on how things will change during a human lifetime or even ten or twenty of them. On a timescale of decades, most of the variation is due to changes in solar activity, CO2 concentrations and aerosol concentrations.
I don’t know of any physical reason to suspect that the characteristics of the internal variation would throw us wildly off course, statistically. Do you?
Scientist,
The trend over the thirty year period is only statistically significant when tested against certain sorts of null hypotheses – in particular, those with low or zero long-term autocorrelation. That’s an assumption. It might be true, but given internal variability stuff like the Pacific decadal oscillation, Atlantic multi-decadal oscillation, interstadials, and so on (look ’em up), all working on decadal timescales or longer, it probably isn’t.
The question is: “is the climate flat?” You have to prove it before you can make such statements as “On a timescale of decades, most of the variation is due to changes in solar activity, CO2 concentrations and aerosol concentrations”. How do you know? What’s the evidence? I’m not saying there isn’t any, but the only evidence I’ve seen presented is that the models come out flat if you don’t add CO2, which is a bit too virtual for my taste.
Take the Medieval warm period. http://www.jennifermarohasy.com/blog/archives/002711.html Many reconstructions of past temperature show the temperature went up during the first millennium, then dropped during the little ice age, and then started rising again some time during the 19th century. Which forcing caused it: solar activity, CO2 concentrations or aerosol concentrations? How about the Roman warm period, or older Dansgard-Oeschger events? Can you nail down exactly what did cause each of them well enough to be able to say the same sort of effects don’t still apply? Note, I’m not saying that this proves that CO2 isn’t causing the current warming, just that the null hypothesis you have to compare things against isn’t flat.
Seriously, go plot that cumulative coin-toss example I mentioned, look at a few runs until you get the general idea of how it behaves, and then figure out for yourself how you would test if the coin was fair. How many coin tosses would you need? And ask yourself, do those graphs look at all like temperature graphs? How would you go about telling the difference?
“And trying to claim anything based on temperatures since 2001 is also not useful.”
And since you also commented on that utilizing temperatures around 1998 isn’t useful, you have a ten year period in which you’re stating that the record is not reliable. Now the difficulty I have with this is that you say that a thirty year period IS reliable – however, understanding as I do that the accuracy of a statistical model increases logarithmically, not linearly, with respect to the sample size, I’m a little skeptical of this claim. I’m a little more skeptical because, if we using a year as a data point, a sample size of thirty with as much internal variability as temperatures doesn’t even begin to approach accurate. Statistically, you can’t even say temperatures aren’t declining.
That’s if you take a proper approach to data points, which most if not all climate models fail to – they treat locations or regions to lesser or greater extents as data points, which only works if the variable being measured is independent from point to point, which temperature very plainly is not (That is, you can’t eliminate uncertainty by increasing the number of data points when your data points can to a great extent be derived from one another). I’d have to either integrate a very nasty equation or pull out a chart to tell you exactly how accurate a statistical model based on thirty data points (this isn’t accurate, and is in fact hyperbole – they do get a great deal more data points than that, because the dependence of data points can be calculated and accounted for, particularly as they have developed other models which do a pretty good job of calculating and accounting, but there’s a considerable layer of uncertainty involved there, as well) with extremely high internal variability would be, and I’d rather not, so you’ll just have to take my word for it that it is not in fact all that good. If you want a very good demonstration of the problem, plot annual temperature change over the last decade; the average will come out negative, but with extremely high inaccuracy. And remember, thirty years is not three times as good as ten years, and, while I don’t feel like breaking out the charts, it would really surprise me if the accuracy were even doubled (as measured by halving the uncertainty). Strong variation != strong evidence, particularly in a system where the total trend is less than the noise.
“I don’t know of any physical reason to suspect that the characteristics of the internal variation would throw us wildly off course, statistically. Do you?” is an argument from personal incredulity, and is, quite bluntly, faulty. You say temperatures don’t vary this much on a scale of decades, historically – well, considering the quite considerably “blurriness” of historical records, this is a completely unfounded assumption. By blurriness, I refer to the fact that there are no historical measurement devices known that give high accuracy of even annual temperatures; you can’t go through an ice core and say that in the year 1507 BC the temperature at this location was 21 below zero, nor can you with any degree of accuracy make distinctions between years (i/e, this year was three degrees colder than the previous one). Trees are no more accurate, because the temperature markers vary considerably with other variables as well, such as sunlight and carbon dioxide levels. So, in the spirit of your claim – I don’t know of any physical evidence to even say what is normal course, statistically. Do you?
the only evidence I’ve seen presented is that the models come out flat if you don’t add CO2, which is a bit too virtual for my taste. – that is a very long way from being the only evidence that CO2 affects climate. This knowledge comes from very basic physics. CO2 absorbs IR. Its concentration in the atmosphere is high enough that it plays a significant role in the energy balance of the atmosphere. Its concentration is rising with a doubling time of many decades. So therefore, its effect on climate will be seen over that timescale.
I think that saying the models come out flat without the addition of CO2 is looking at it the wrong way round. Rather, physically, it’s impossible to add as much CO2 to the atmosphere as we have done without seeing temperatures rise, unless some other effect is counteracting the effect of CO2.
As an aside I don’t fully understand why people often don’t like models, because there really is no division between scribbling equations on a page to solve simplified equations of radiative transfer (which essentially represents an extremely simple model), and writing a computer program to solve a more complicated case, with changing compositions and motions, which you can’t solve by hand.
I don’t really understand your coin toss analogy or how it relates to temperature trends. Seems like you’re trying to compare apples with oranges.
Adirian – no, I said nothing about unreliable, anywhere. It’s really pointless to discuss things if you’re going to just invent random claims like that. The record is quite reliable. The issue is separating short term unforced variation from long term forced variation. You can do the calculations yourself – take a ten year period in the climate record, fit a linear trend to it, calculate the error on your coefficients. Now do the same for a 30 year period. Please do that and you can see why ten years is too short and thirty years is not too short a period to derive a trend from.
Scientist: Try several different 30 year periods and see how the trends differ. Just looking at the graphs, 1978 to 2008 should be rising, but 1938 to 1968 looks like it will come out flat or slightly falling. I very much doubt you can explain the difference between those periods can be explained by variations in fossil-fuel-derived CO2 plus the much shorter El Nino and sunspot cycles. So there are other factors involved that show up on a 30 year time scale. OTOH, if you go to a hundred-year time scale, you start seeing the recovery from the little ice age…
Scientist,
When I said “the only evidence I’ve seen presented” I meant the only evidence for the climate being flat. The evidence for claiming that on a timescale of decades, most of the variation is forced and not due to internal variability. I wasn’t talking about evidence that CO2 affects climate, but the claim that nothing else does.
Yes. I already know the very basic physics. Doubling CO2 would, all other things being equal, increase the temperature by about 1.1 C. And the increase from 280 to 380 we saw over the 20th century would increase it by about half that, so we can expect the temperature in 2100 to be about 0.5 C above what it is today as a result of CO2. But all other things are not equal. The modellers posit all sorts of other mysterious effects causing positive feedback that increases this 1.1 C to a variety of numbers ranging from 3 C to 10 C and beyond. And which would incidentally imply that we should have had between 1.5 C and 5 C rise over the 20th century, which they then have to invent more mysterious effects to cancel. Water vapour and aerosols and ocean heat capacity and all that jazz. But we don’t even know from observation the sign of the feedback, let alone that it has the huge values the modellers claim.
But what I’m talking about is a different feature of the models, that if you don’t put in external forcers like AGW or massive solar changes, they come out nearly flat on a decadal timescale. This, it is claimed, is evidence that the climate is naturally flat, and therefore any lumps and bumps in it must be unnatural. But I don’t accept computer models as evidence of flatness in the real world. History begs to differ.
I suspect some of the flatness is due to the way the modellers deal with divergence. Here is some of the output of that climate model the BBC got everyone to run at home. http://www.climateprediction.net/science/thirdresults.php http://www.climateprediction.net/science/secondresults.php What they do is to trim out the obviously crazy stuff and quietly bin it, and then take the spread of the remainder as representative of the uncertainty while they draw a line through the middle of it. And of course if you do that, any variations on a decadal timescale that you might be modelling get cancelled out. It is like taking all those cumulative coin toss graphs, averaging them, and finding the line goes flat. Correct, in a sense, but it isn’t how an actual climate behaves.
Take a monthly temperature series and plot the anomaly for each month against the anomaly of the next month. That is, if you have temperatures a, b, c, d, e, f, … then plot the points (a,b), (b,c), (c,d), (de,e),… You will see that the resulting patch is not circular but elongated along the diagonal. The temperatures are autocorrelated. There are an infinite number of possible mechanisms for autocorrelated random processes (look up ARIMA and ARFIMA processes sometime) and the coin toss experiment is only one of them. (ARIMA(1,1,0) to be precise.) It’s just an easy way to get an intuitive understanding of what utter havoc autocorrelation can play on statistical tests that assume stuff is “independent identically distributed”. It’s not often taught outside postgrad stats and econometrics courses, I only came across it myself later on in my professional life, but it is vitally important for every scientist to know about.
Scientist,
Congratulations!
You’re reasonable exchange with Stevo is the first positive contribution that you’ve made to this blog. I actually paid attention to what you said!
Argh! Your.
BillBodell – what a pointless interjection.
Stevo – sorry I misunderstood what you were saying. But I don’t think anyone has said climate variations would be zero without CO2 – far from it. Everyone knows that solar activity changes, that volcanoes erupt, and things like that. Look up papers by Solanki et al for work on how solar variation has been an important driver in the past. In the absence of all forcing, of course the climate variation would be essentially flat – that’s just Newton’s first law, really.
I don’t know why you think feedback effects are mysterious. They’re fairly common sense really – if you melt the polar caps a bit, the Earth’s albedo drops, so more radiation is absorbed. What’s mysterious about that? And as oceans get warmer, they can hold less CO2. No mystery there, surely?
Here‘s a paper about autocorrelation and climate change that you might be interested in.
markm – there is no such thing as ‘recovery from the little ice age’. The climate doesn’t have an equilibrium state that it must return to. It won’t change without being pushed. And climate change over the 20th century is well explained by a combination of rising CO2, variable aerosols and solar activity, and the occasional large volcanic eruption.
Whoever ‘scientist’ is, it is clear he is not a scientist. He is ignorant of basic scientific processes, and his last post has an amazing number of errors for its length.
(a) “In the absence of forcing climate variation would be flat”. He does not appear to have heard about nonlinear systems and chaos. Complicated nonlinear systems such as climate can fluctuate in an irregular way even with constant forcing. (I assume he means constant forcing, not no forcing, which would require switching the sun off).
(b) “that’s just Newton’s first law really”. Go back to school and learn Newton’s laws.
(c) If the positive feedback process he mentions really occurs, it would have happened already, regardless of any man-made or natural heating. This is what scientists call an instability – like a pencil balanced on its point – you don’t need to push the pencil for it to fall over. That is what is mysterious about feedback. The feedback must be negative – otherwise we wouldn’t be here.
(d) “climate change is well explained by …”. Nonsense. The early 20thC rise is just as rapid as the late 20thC, despite much lower CO2 emissions. The “aerosol” “explanation” for the 1940-70 cooling is a joke. The proper scientist, like Steveo and markm, realizes that there are many things we don’t understand. The bogus scientist pretends he understands everything.
The main point is, as our host says, that the latest observations show a leveling off, contrary to the predictions of the alarmists. No doubt, the alarmists will soon invent another man-made “explanation” for this – I can’t wait to see what garbage they come up with.
Yeah, you might want to check on the definition of ‘forcing’. And you might want to try a more convincing rebuttal than ‘it’s a joke’. Evidence? Papers?
You also obviously don’t understand feedback. You must be either ignorant of or in denial of all the evidence that shows that feedbacks exist in our climate system.
No, the latest observations do not show a levelling off. To think that they do, you have to have no understanding of trends and statistics.
Scientist,
You say “On a timescale of decades, most of the variation is due to changes in solar activity, CO2 concentrations and aerosol concentrations.” which I took to imply that you thought internal variation was negligible on a decadal timescale. I cited examples of internal variation like the Pacific decadal oscillation that do occur on a decadal timescale in answer to that, and pointed out that with autocorrelated sequences even the noise can occur on arbitrarily large timescales.
Now you say “But I don’t think anyone has said climate variations would be zero without CO2 – far from it.” So which is it? Are internal variations effectively zero on a decadal timescale or not?
“In the absence of all forcing, of course the climate variation would be essentially flat – that’s just Newton’s first law, really.” So now you are claiming it’s flat?
On what basis? What’s the evidence for the claim that, absent changes in forcing, climate would be flat on a decadal timescale? If you think you can argue that from Newton’s first law, I’d like to see it.
BTW, when I say ‘mysterious’ I mean that there are still many mysteries about them. We don’t understand the quantitative (and sometimes qualitative) details. And of course there are feedbacks in the system, but there are negative feedbacks too. What do they all add up to? Nobody knows. For all we know, the total might even be negative, and doubling CO2 could give less than a degree.
Now you say “But I don’t think anyone has said climate variations would be zero without CO2 – far from it.” So which is it? – I’m extremely unimpressed that you’d take my words out of context to distort what I was saying. Are you interested in reasonable discussion or just looking to make cheap points?
If you want to clarify what you meant, please do.
We were discussing whether there was internal variability in the climate on a decadal timescale. In order to deduce that any change on such a timescale is due to changes in external forcing, you have to assume or have evidence that internal forcing is negligible on that timescale – you have to have a particular form of null hypothesis. I’ve discussed various reasons for why that’s unlikely to be true, and stated that the only ‘evidence’ I’ve seen presented for it has been graphs that show model results with and without added CO2, for which the ones without were flat. (The models did include natural forcings like volcanoes and solar changes, but according to the model the differences were insignificant.)
This is a crucial plank on which your argument rests. If there may be unquantified spurious trends on a decadal timescale due to internal variation, then performing regression on a 30-year base is no better supported than doing one on 10 years, 60 years, 1 year, or 8,000 years.
Rather than come up with an answer to that, you said that you didn’t think anyone had made the claim that I had attacked, and on which your whole argument relies. Or so I understood. Were you merely objecting that the only forcing I had mentioned in one particular sentence was CO2? If so, I’ll concede the point that I said CO2 as a stand in for the whole collection without making that clear, if you’ll agree that your comment hasn’t in any way answered the essential point of my argument.
And before you jump to the conclusion that I’ve intentionally tried to distort what you said, you should please bear in mind that in a conversation where people are struggling to understand what the other means, and coming from opposite ends of a polarised and somewhat rancorous political spectrum, that genuine misunderstandings are common.
For example, I said “the only evidence I’ve seen presented is that the models come out flat if you don’t add CO2, which is a bit too virtual for my taste.” and you responded with “that is a very long way from being the only evidence that CO2 affects climate.” I was talking about the evidence that it was flat, and you twisted it to mean the evidence it was affected by CO2. You then went on to explain, in what might be seen as a very patronising manner, that the CO2 greenhouse effect was a matter of basic physics, as if I wouldn’t know that. It looks like a strawman argument put up to avoid the issue of the evidence for flatness, and at the same time to portray me as a fool for not being aware of the most basic physical argument that appears in every single presentation of AGW, even those to the youngest of schoolchildren. That, at least, is how somebody could interpret it, if they weren’t feeling generous.
Now I’m not complaining, and I did assume that it was simple misunderstanding. I only put up this explanation in the hopes that you can see how genuinely unintended misunderstanding can easily look like dishonest debating techniques.
I’ve found our exchange interesting, although not particularly fruitful. And it’s been better than a lot of such exchanges I’ve had with AGW believers. But I have noticed that you still have a tendency to treat your opponents as if they were ignorant fools for believing as they do. That sort of rhetorical tactic can work in an environment where most people believe as you do, and you are to some degree playing to the gallery. But here you are on what might be called ‘enemy turf’, and if your purpose is either to persuade, or merely to have a reasonable debate, you should be aware that the psychology of such situations is that belittling people’s views and intellects leads people to fight you rather than listen. It is best that even if criticised yourself, that you contain your answer to the bare facts, without editorial. It works better in the long run. Maybe you’re not bothered by that, or of what people here have come to think of you, and I’ve no personal objection to you using such tactics since it makes our position look far more persuasive in comparison, but perhaps it’s something you’d want to think about.